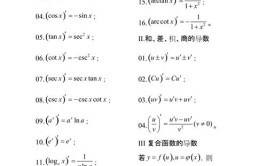主要性质：定义域x∈R；值域[-1，1]。单调性：在[(2k-1)π，2kπ]，k∈Z上是单调增函数，在[2kπ，(2k 1)π]，k∈Z上是单调减函数。周期性：T=2π(与正弦函数相同)。对称性：既是轴对称图形，又是中心对称图形。对称轴：关于直线x=kπ，k∈Z对称；中心对称：关于点(kππ/2，0)，k∈Z对称。

奇偶性：偶函数(其图像关于Y轴对称)。最值和零点：最大值：当x=2kπ，k∈Z时，y(max)=1；最小值：当x=2kπ-π，k∈Z时，y(min)=-1。零值点：(kππ/2，0)，k∈Z。

余弦函数，三角函数的一种。在Rt△ABC（直角三角形）中，∠C=90°，∠A的余弦是它的邻边比三角形的斜边，即cosA=b/c，也可写为cosa=AC/AB。余弦函数：f(x)=cosx（x∈R）。余弦定理：三角形任一边的平方等于另两边的平方和减去这两边与其夹角余弦值的二倍。

余弦函数公式：半角公式：cos(A/2)=±√((1+cosA)/2)；倍角公式：Cos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1；两角和与差公式:cos(A+B)=cosAcosB-sinAsinB、cos(A-B)=cosAcosB+sinAsinB。