-
为什么罗尔定理是对的
数学,作为人类智慧的结晶,历经数千年而不断进化。在这漫长的历史进程中,众多数学家为我们留下了丰富的理论成果。罗尔定理,便是其中一颗璀璨的明珠。本文将从罗尔定理的提出背景、定理内容、证明过程以及现实意义...
-
勾股之学是出自什么地方
在中国,周朝时期的商高提出了“勾三股四弦五”的勾股定理的特例。在西方,最早提出并证明此定理的为公元前6世纪古希腊的毕达哥拉斯学派,他用演绎法证明了直角三角形斜边平方等于两直角边平方之和。相关介绍勾股定...
-
射影定理是哪年级学的
射影定理是初三学的。射影定理,又称“欧几里德定理”:在直角三角形中,斜边上的高是两条直角边在斜边射影的比例中项,每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。射影定理是数学图形计算的...
-
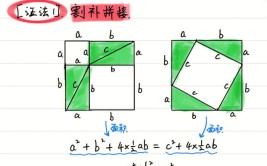
勾股定理的证明方法
做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三个边长分别为a、b、c的正方形,把它们拼成两个正方形.可以看到,这两个正方形的边长都是a+b,所以面积相等.即a的平方加b的...