-
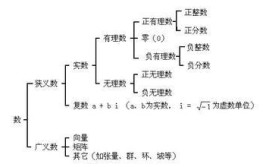
复数的几何意义
复数的几何意义,是指复数z=a+bi(a、b∈R),一一对应复平面内的点Z(a,b)。其中,在复平面内,复数的实部(a)是其对应点的横坐标,复数的虚部(b)是其对应点的纵坐标。复数z=a+bi(a、b...
-
实数与虚数的区别
实数和虚数的区别包括数学性质不同和表示方式不同。其中,实数是有理数和无理数的总称。数学上,实数定义为与数轴上的实数,点相对应的数。虚数就是形如a+b*i的数,其中a、b是实数,且b≠0,i²=-1。虚...
-
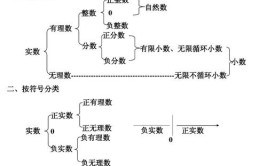
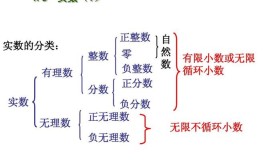
什么是实数?实数包括什么数?
实数,是有理数和无理数的总称。数学上,实数定义为与数轴上的实数,点相对应的数。实数可以直观地看作有限小数与无限小数,实数和数轴上的点一一对应。实数由一个五元组(R,+,0,×,1,≤)定义,其中,R是...
-
有理数和实数的区别
有理数与实数的区别:性质不同;有理数:有理数为整数(正整数、0、负整数)和分数的统称。正整数和正分数合称为正有理数,负整数和负分数合称为负有理数。因而有理数集的数可分为正有理数、负有理数和零。实数:实...
-
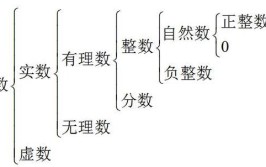
复数包括实数和虚数吗
复数包括实数和虚数。复数是由意大利米兰学者卡当在十六世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受。相关介绍我们把形如z=a+bi(a,b均为实数)的数称为复数,其...