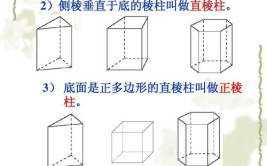
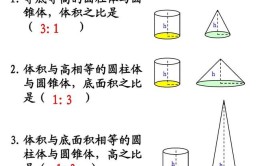
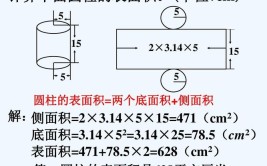
圆锥体积的公式是:V=1/3Sh(V=1/3πr²h),其中π为圆周率,约等于3.14,S是底面积,h为圆锥的高,r是底面半径。
圆锥是一种几何图形,是以直角三角形的直角边所在直线为旋转轴,其余两边旋转而成的曲面所围成的几何体叫做圆锥。
例题:一个圆锥形沙堆,底面周长是12.56米,高6米,将这些沙铺在宽10米的道路上铺4厘米厚,可以铺多少米长?
(图片来自网络侵删)
解答:可以铺62.8米长。因为题目是要求用这堆沙子铺多少米长,那么首先求得沙堆的体积,沙堆的形状是圆锥形的,利用圆锥的体积计算公式求得体积,再进一步再求铺多少米长:
⅓×3.14×(12.56÷3.14÷2)2×6
=⅓×3.14×22×6
=3.14×4×2
=25.12(立方米);
可以铺:
25.12÷(10×0.04)
=25.12÷0.4
=62.8(米)
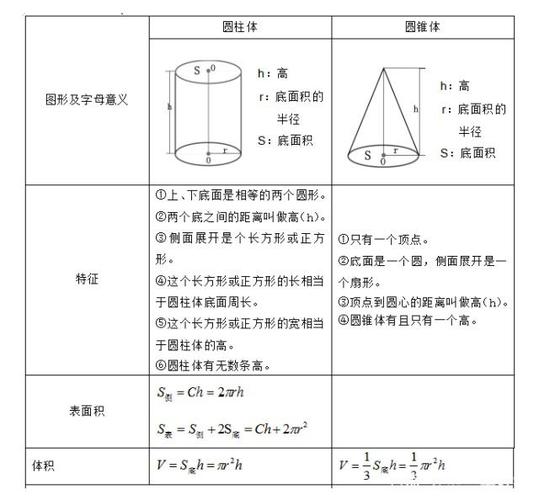
圆锥的计算公式:S表面积=πr^2+πrR,r是底面半径,R是母线。
S侧面积=πrR,r是底面半径,R是母线。
V体面积=1/3Sh,S是底面积,h是圆锥高。
弧长:nπR/180扇行面积:nπR^2/360。
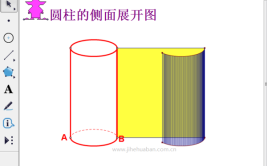
侧面展开图弧长=底面圆周长=2πr=πd。
侧百展开图面积=1/2x2πrl=πrl。
例题:已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽,(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是多少?
解答:设这块扇形铁皮的半径为Rcm;圆锥的底面周长等于它的侧面展开图的弧长,360/270x2πR=2πx2/60,解得R=40。