有界性：L1≤y≤L2(L1,L2是常数)，顾名思义就是函数值在某一个有限的范围内，即L1≤y≤L2，其中L1;L2是常数。注意：①L1为下界，L2为上界;②上界与下界同时存在才称之为有界 ;③要看清楚题目中所给的范围。

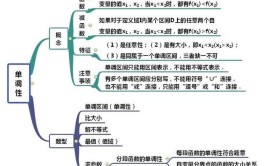
函数除了有两个重要要素：定义域与解析式以外。还有四个性质，分别是：有界性;单调性;奇偶性;周期性。要知道这四个性质是针对函数的函数值而言的。

有界性

有界性：L1≤y≤L2(L1,L2是常数)

顾名思义就是函数值在某一个有限的范围内，即L1≤y≤L2，其中L1;L2是常数。

注意：

①L1为下界，L2为上界

②上界与下界同时存在才称之为有界

③要看清楚题目中所给的范围

例如

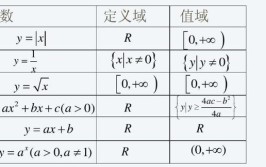
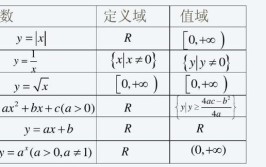
(1)y=sin x 在定义域上是有界的。因为其对应的函数值都会满足：-1≤y≤1。

(2)y=ln x在定义域上是无界的。因为其对应的函数值都会满足：y∈R。

但在定义域内的任何一个有限区间。如 (1,5)上，函数则是有界的。因为其对应的函数值都会满足：

单调性

单调性：x1

两种情况：单调递增或者单调递减。

若对区间 Ⅰ 内的任意两个变量x1

若对区间 Ⅰ 内的任意两个变量x1f(x2)，则函数在区间 Ⅰ 上是单调递减的;通俗理解自变量增大时，对应的函数值变小，则函数为减函数。

注意：

①反函数的单调性与原来函数的单调性相同

②复合函数的单调性满足"同为增，异为减"

例如

已知函数 f 在 R 上是单调递减的，那么 y=f(x2)在(-∞，0)上是单调递增，在(0，+∞)上是单调递减。

奇偶性

奇偶性：f(x)=-f(x);f(x)=f(-x)

前提条件：函数的定义域要关于原点对称，即若x∈D 则-x∈D。

偶函数：若f(x)=f(-x);

等价定义形式：f(x)=f(-x) <=> f(x)-f(-x)=0 <=> f(x)÷f(-x)=1;

奇函数：若f(x)=-f(-x);

等价定义形式：f(x)=-f(-x) <=> f(x)+f(-x)=0 <=> f(x)÷f(-x)=-1;

注意：

①判断函数奇偶性只需要找到f(x)与f(-x)之间的关系即可

②奇函数加上偶函数得到的是非奇非偶函数

③反函数的奇偶性与原来函数的奇偶性相同

例如

函数 y = sin x 是奇函数，

y = cos x 是偶函数，

那么 y = arcsin x 是奇函数;

y = arccos x是偶函数;

y = sin x + cos x 非奇非偶函数。

周期性

周期性：f(x)=f(x+L) 周期为L

如果存在一个正数L，可以对函数 f(x) 定义域 D 内的每一个数 x 都有：则函数f(x)的周期为 L。

注意：

①判断函数周期性只需找到可以满足 f(x) = f(x+L) 的正数 L 即可

②所学的各类函数中只有三角函数有周期性