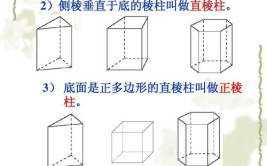
1、中心原子不同

四面体是指中心原子在四面体体心。

三角锥中的中心原子在顶角上。

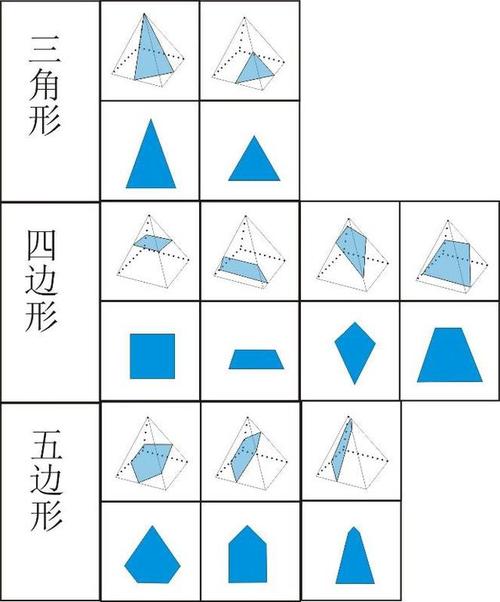
2、原子个数不同

虽然都是外形都是四面体，但四面体型的分子有五个原子。

三角锥的分子只有四个原子。

3、四面体和三角锥都是sp³杂化

三角锥形分子一般由四个原子组成，中心原子sp³杂化（有一对孤电子对），中心原子处于另外三原子构成平面之外，如NH₃等。

而四面体一般由五个原子构成，中心原子sp³杂化，中心原子处于其他四原子构成的四面体的中心，如一氯甲烷，二氯甲烷等。

外心

若O是△ABC的外心，则OA=OB=OC。由于OP⊥平面ABC（射影的定义），因此OP⊥OA、OP⊥OB、OP⊥OC。勾股定理得PA=PB=PC。又tanPAO=OP/OA，tanPBO=OP/OB，tanPCO=OP/OC，由此可知∠PAO=∠PBO=∠PCO。

综上，可得到以下定理：

1.当三棱锥的三条侧棱相等时，顶点在底面的射影是底面三角形的外心。

2.当三棱锥的三条侧棱与底面所成角相等时，顶点在底面的射影是底面三角形的外心。

内心

若O是△ABC的内心，则O到三边距离相等，且O在△ABC内。设O到BC、AC、AB的垂线段分别为OD、OE、OF，那么OD=OE=OF。由勾股定理得PD=PE=PF。又tanPDO=OP/OD，tanPEO=OP/OE，tanPFO=OP/OF，因此∠PDO=∠PEO=∠PFO。且由三垂线定理可知PD⊥BC、PE⊥AC、PF⊥AB，即∠PDO、∠PEO、∠PFO分别是二面角P-BC-A、P-AC-B、P-AB-C的平面角。

综上，可得到以下定理：

1.当三棱锥的顶点到底面三角形三边距离相等，且顶点在底面的射影在底面三角形的内部，那么射影是内心。

2.当三棱锥的各个侧面与底面构成的二面角相等，且顶点在底面的射影在底面三角形的内部，那么射影是内心。

1、三角锥体积V=1/3*S*h，其中S是底面积，h是高。

2、三角锥体积=1/3 S（三角柱的体积）

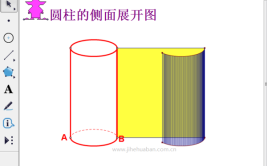
三角锥的底面周长：C=2πr（r：底面半径）

三角锥的表面积：圆锥的表面积由侧面积和底面积两部分组成。全面积（S）=S侧+S底

S侧=πrl+πr^2（r：底面半径，l：圆锥母线)