首先,应力和应变是建筑力学中的基本概念。应力表示单位面积内的力,用σ表示;而应变则是物体单位长度的变形量,用ε表示。这两者之间的关系可以通过胡克定律来描述:σ = Eε,其中E是弹性模量,代表物体在弹性阶段内抵抗形变的能力。
例如,考虑一根金属杆在受到拉力时的情况。通过测量杆上的应力和应变,我们可以利用胡克定律计算出该金属的弹性模量,从而了解其在不同受力情况下的形变特性。
其次,平衡条件也是建筑结构分析中的核心要素。这包括力的平衡和力矩的平衡。力的平衡条件可以表示为ΣF=0,即所有作用在结构上的力之和为零;力矩的平衡条件可以表示为ΣM=0,即所有力矩之和为零。
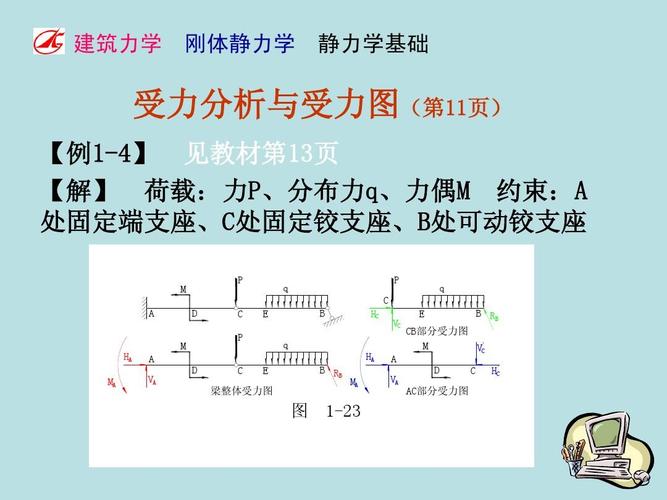
(图片来自网络侵删)
以一个简单的桥梁结构为例,我们需要考虑桥梁自重、车辆荷载、风荷载等多种力的作用。通过力的平衡条件,我们可以计算出桥梁各部分的支撑力和反作用力,确保桥梁在受力时保持平衡。同时,利用力矩的平衡条件,我们可以分析桥梁在受到弯矩作用时的受力情况,从而设计出合理的截面形状和尺寸。
此外,杨氏模量公式也是建筑结构分析中常用的一个公式。它描述了材料的弹性性质,即应力与应变之间的关系。公式为E = σ/ε,其中E为杨氏模量。通过测量材料的应力和应变,我们可以计算出杨氏模量,从而了解材料的弹性性能。
最后,对于承受弯曲作用的梁结构,我们可以利用梁的弹性挠曲公式来计算其挠曲量。这个公式基于梁的材料特性和几何形状推导而来,可以帮助我们预测梁在受力时的变形情况,从而进行合理的设计和加固。
综上所述,建筑力学分析涉及多个关键公式和概念。通过应用这些公式和概念,我们可以对建筑结构进行深入的力学分析,确保其在各种受力情况下的稳定性和安全性。同时,这些分析也有助于我们优化结构设计,提高建筑的性能和耐久性。