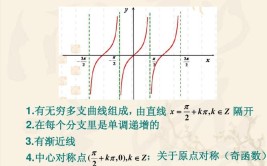
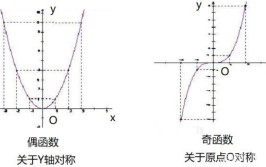
可微与可导的唯一区别:一元函数中可导与可微等价,它们与可积无关,多元函数可微必可导,而反之不成立。
相关介绍例如:
设y=f(x)是一个单变量函数, 如果y在x=x[0]处存在导数y'=f'(x),则称y在x=x[0]处可导。

(图片来自网络侵删)
如果一个函数在x[0]处可导,那么它一定在x[0]处是连续函数
如果一个函数在x[0]处连续,那么它在x[0]处不一定可导
函数可导定义:
1、若f(x)在x0处连续,则当a趋向于0时, [f(x+a)-f(x)]/a存在极限, 则称f(x)在x0处可导
2、若对于区间(a,b)上任意一点m,f(m)均可导,则称f(x)在(a,b)上可导