-
如何判断函数是否可导
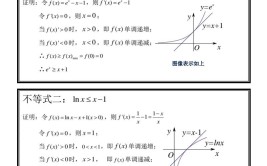
设y=f(x)是一个单变量函数,如果y在x=x0处左右导数分别存在且相等,则称y在x=x0处可导。如果一个函数在x0处可导,那么它一定在x0处是连续函数。1、设f(x)在x0及其附近有定义,则当a趋向...
-
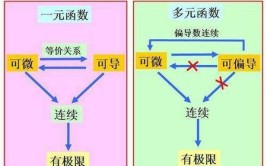
可微与可导的区别
可微与可导的唯一区别:一元函数中可导与可微等价,它们与可积无关,多元函数可微必可导,而反之不成立。相关介绍例如:设y=f(x)是一个单变量函数,如果y在x=x[0]处存在导数y'=f'...
-
洛必达法则可以连续求导两次吗
可以。洛必达法则是在一定条件下通过分子分母分别求导再求极限来确定未定式值的方法。众所周知,两个无穷小之比或两个无穷大之比的极限可能存在,也可能不存在。因此,求这类极限时往往需要适当的变形,转化成可利用...
-
讨论可导性要先讨论连续性吗
在一阶导数阶段,可导必连续。只要看到可导就可以想到必连续,但是连续不一定可导,比如尖点,无穷点之类。至于为什么看一下导数定义和连续定义,还有间断点定义,按照一阶导数定义如果不连续导数也不成立了,极限发...
-
0的导数是什么
0的导数是0,任何常(函)数的导数为0。不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的...
-
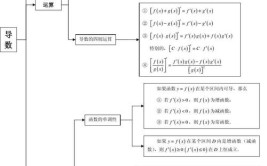
连续可导和导数连续的区别
表现形式不同:函数连续是此函数的图像是连续的曲线,没有间断点。导函数连续是此函数的图像是光滑的,没有尖点。(图片来自网络侵删)函数在该处的极限等于函数在该处的取值相关介绍关系不同:可导,导数不一定连续...