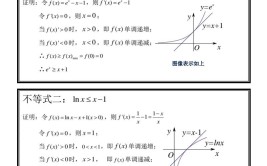
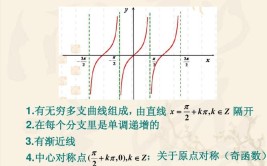
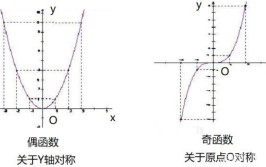
设y=f(x)是一个单变量函数，如果y在x=x0处左右导数分别存在且相等，则称y在x=x0处可导。如果一个函数在x0处可导，那么它一定在x0处是连续函数。1、设f(x)在x0及其附近有定义，则当a趋向于0时，若[f(x0+a)-f(x0)]/a的极限存在，则称f(x)在x0处可导；2、若对于区间(a，b)上任意一点m，f均可导，则称f(x)在(a，b)上可导。

函数的定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同。

函数是发生在集合之间的一种对应关系。然后，要理解发生在A、B之间的函数关系有且不止一个。最后，要重点理解函数的三要素。

函数的对应法则通常用解析式表示，但大量的函数关系是无法用解析式表示的，可以用图像、表格及其他形式表示。