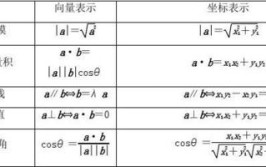
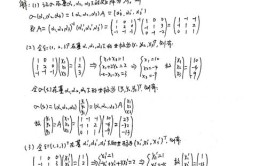向量组的行列式等于0,
那就说明通过线性变换可以得到向量组之间的关系为:
k1*a1+ k2*a2+ ··· + km*am=0,k1, k2, ···,km为不全为零的数

(图片来自网络侵删)
所以此向量组就是线性相关的
相关介绍注意:
对于任一向量组而言,,不是线性无关的就是线性相关的。
向量组只包含一个向量a时,a为0向量,则说A线性相关; 若a≠0, 则说A线性无关。
包含零向量的任何向量组是线性相关的。
含有相同向量的向量组必线性相关。
增加向量的个数,不改变向量的相关性。(注意,原本的向量组是线性相关的)
减少向量的个数,不改变向量的无关性。(注意,原本的向量组是线性无关的)
一个向量组线性无关,则在相同位置处都增加一个分量后得到的新向量组仍线性无关。
一个向量组线性相关,则在相同位置处都去掉一个分量后得到的新向量组仍线性相关。 [2]
若向量组所包含向量个数等于分量个数时,判定向量组是否线性相关即是判定这些向量为列组成的行列式是否为零。若行列式为零,则向量组线性相关;否则是线性无关的。