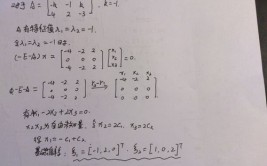二重特征值是指特征值是特征多项式的2重根。
如A的特征多项式为|λE-A |=(λ-2)(λ^2-8λ+18+3a)。
当λ=2是特征方程的二重根,则有2^2-8*2+18+3a=0,解得a=-2。
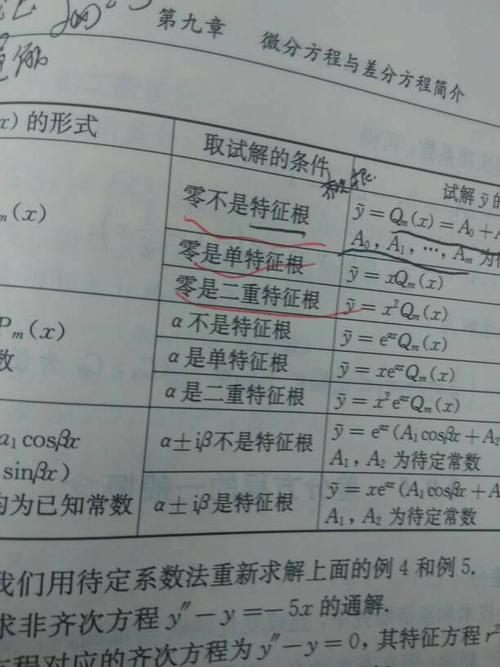
(图片来自网络侵删)
若λ=2不是特征方程的二重根,则(λ^2-8λ+18+3a)为完全平方,从18+3a=16而,解得 a。
设 A 是n阶方阵,如果存在数m和非零n维列向量 x,使得 Ax=mx 成立,则称 m 是A的一个特征值或本征值。非零n维列向量x称为矩阵A的属于(对应于)特征值m的特征向量或本征向量,简称A的特征向量或A的本征向量。
相关介绍特征值的基本应用:
1、求特征向量:
设A为n阶矩阵,根据关系式Ax=λx,可写出(λE-A)x=0,继而写出特征多项式|λE-A|=0,可求出矩阵A有n个特征值(包括重特征值)。
将求出的特征值λi代入原特征多项式,求解方程(λiE-A)x=0,所求解向量x就是对应的特征值λi的特征向量。